Math6003 Hw4

Ex 1

a

For $n=4$, I are asked to solve the linear system using the MATLAB \ command and then evaluate the relative error. First, I construct the matrix $A$ and vector $b$. The points $x_i$ are generated via linspace(0, 1, 4), giving $x = (0, 1/3, 2/3, 1)$. The exact solution $x_e$ for $n=4$ must have a 1 in the position corresponding to the coefficient of $x^2$ and a 1 for the constant term ($x^0$). Since the vander command in MATLAB generates columns in descending order of power ($x^{n-1}, …, x^0$), the exact solution vector is $x_e = (0, 1, 0, 1)^{\top}$. The computed solution is denoted $x_c$. The relative error is then calculated using the formula $\epsilon_{n}=\frac{||x_{c}-x||}{||x||}$, where $x$ is the exact solution.

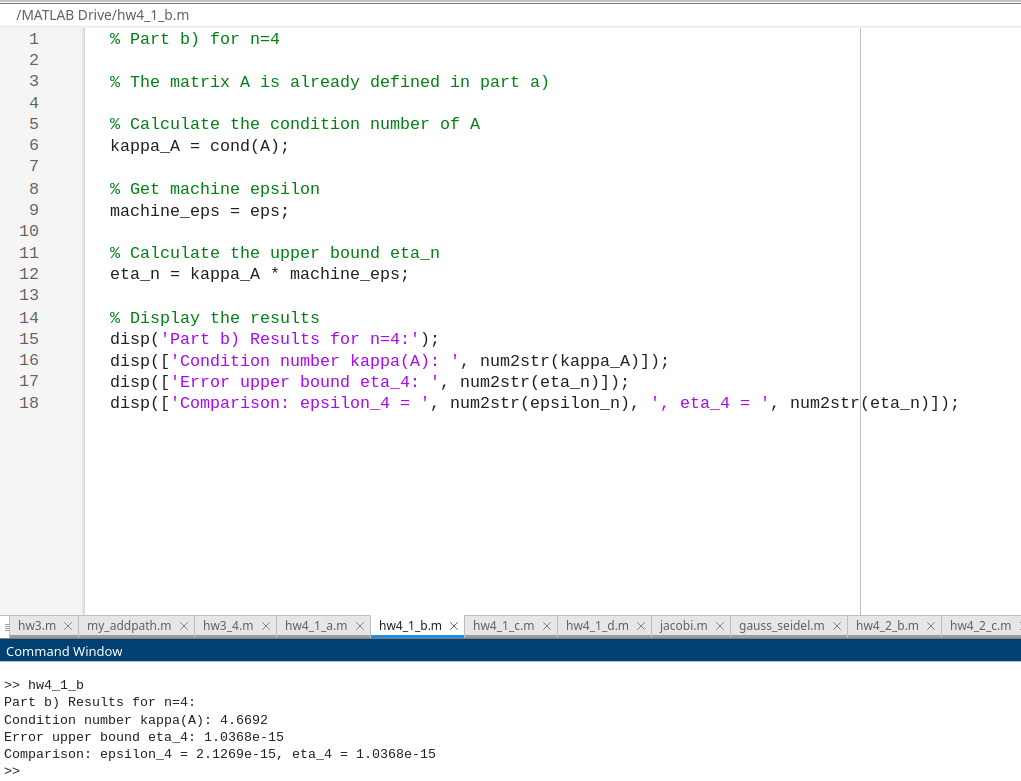
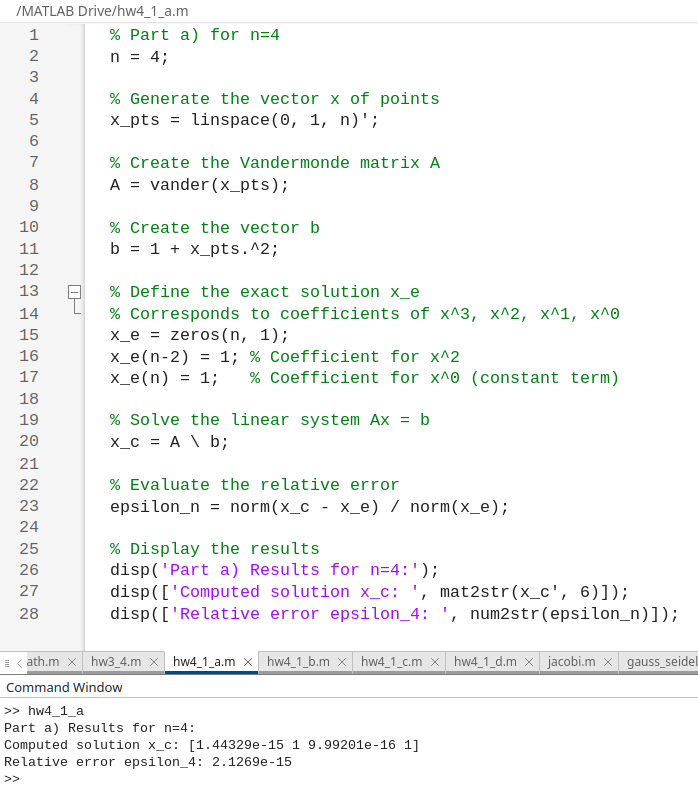
The result of hw4_1_a.m:

### b An upper bound for the relative error is given by $\eta_{n}=\kappa(A) \cdot \text{eps}$ , where $\kappa(A)$ is the condition number of matrix A and `eps` is the machine epsilon, which is predefined in MATLAB. I are asked to compare the relative error $\epsilon_n$ with this bound $\eta_n$ for $n=4$.

The result of hw4_1_b.m

### c This section requires repeating the previous steps for $n=4,6,8,...,20$. I need to visualize the relative error $\epsilon_n$, the upper bound $\eta_n$, and the normalized residual $r_{n}=||b-Ax_{c}||/||b||$ as functions of $n$. The plots should be generated on both logarithmic and semi-logarithmic scales. From these plots, I need to determine the type of growth for the error $\epsilon_n$ and assess if the residual $r_n$ is a good indicator of the error $\epsilon_n$.

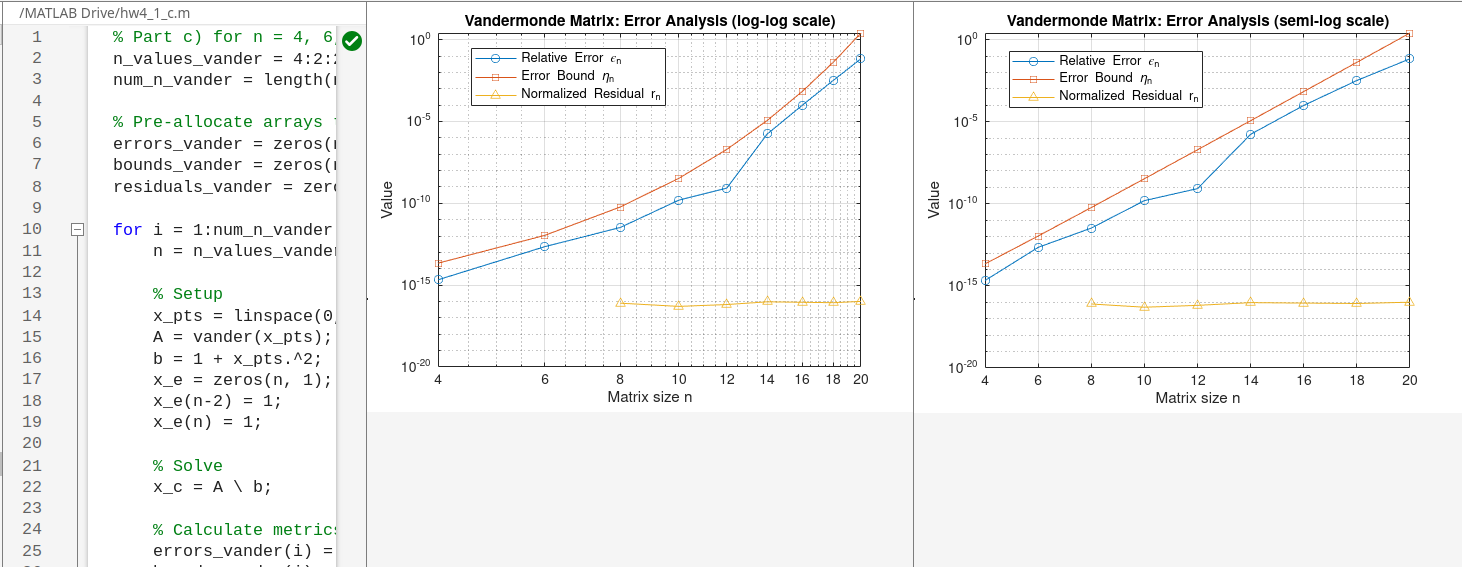
Vandermonde matrices are known to be ill-conditioned, with the condition number growing exponentially with $n$. Therefore, I expect the semilogy plot of $\epsilon_n$ and $\eta_n$ to show straight lines, indicating $\textbf{exponential growth}$. The residual $r_n$ is expected to remain small, close to machine precision, while the actual error $\epsilon_n$ grows large. This would imply that the residual is $\textbf{not a good indicator of the error}$ for this ill-conditioned system.

### d Analysis of a Tridiagonal Matrix} This part requires repeating the analysis from (c) for a different matrix. The matrix is a tridiagonal matrix defined as: $$ A = \begin{pmatrix} 2 & -1 & & & \\ -1 & 2 & -1 & & \\ & \ddots & \ddots & \ddots & \\ & & -1 & 2 & -1 \\ & & & -1 & 2 \end{pmatrix} $$ The analysis should be done for $n=5,10,...,100$. The right-hand side is $b=(2,2,...,2)^{\top}$ , and the exact solution is given by $x_i = i(n-i+1)$. Finally, I are asked to comment on the results.

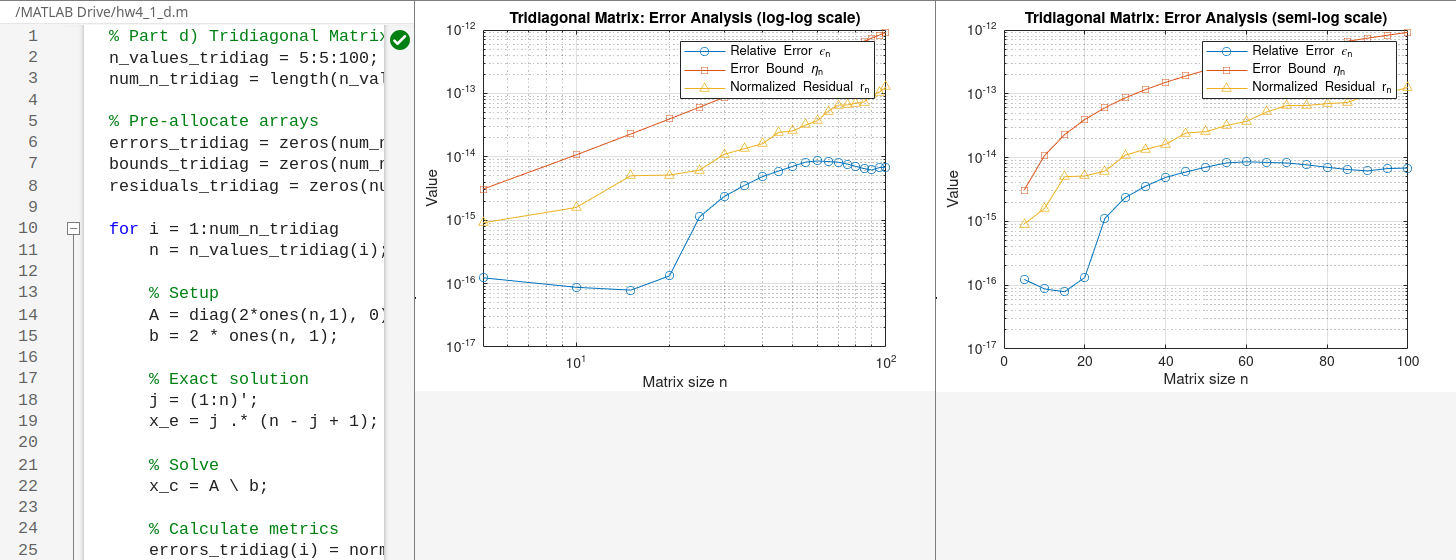
This tridiagonal matrix is well-conditioned. Its condition number grows polynomially with $n$ (like $O(n^2)$). The error $\epsilon_n$ should grow much more slowly than in the Vandermonde case, exhibiting polynomial rather than exponential growth. The residual $r_n$ will be a better, though not perfect, indicator of the true error compared to the previous case.

Comments on the obtained results: - $\textbf{Error Growth:}$ The relative error $\epsilon_n$ for the tridiagonal system grows polynomially with $n$, which is significantly slower than the exponential growth observed for the Vandermonde matrix. This will be visible as a straight line on the `loglog` plot. - $\textbf{Conditioning:}$ The dramatic difference in error behavior is due to the condition number. The Vandermonde matrix is severely ill-conditioned, whereas the tridiagonal matrix is well-conditioned. - $\textbf{Residual as an Error Indicator:}$ For the well-conditioned tridiagonal matrix, the normalized residual $r_n$ and the relative error $\epsilon_n$ have much closer values. The residual is a far more reliable indicator of the true error in this case than it was for the Vandermonde system. ## Ex 2 ### a The task is to complete the files $jacobi.m$ and $gauss\_seidel.m$. These files implement iterative methods based on a matrix splitting $A = P - (P-A)$, where $P$ is the preconditioner. The iterative update can be expressed as $x^{(k+1)} = x^{(k)} + z^{(k)}$, where $z^{(k)}$ is the solution to $Pz^{(k)} = r^{(k)}$, and $r^{(k)} = b - Ax^{(k)}$ is the residual.

For the $\textbf{Jacobi method}$, the preconditioner P is the diagonal of A. For the $\textbf{Gauss-Seidel method}$, P is the lower triangular part of A. The missing lines implement the calculation of the residual, the update step, and the storing of the residual norm at each iteration.

jacobi.m:

function [x, iter, res]= jacobi(A,b,x0,nmax,tol)
% JACOBI iterative method
%   [X, Niter, Res] = JACOBI(A,B,X0,NMAX,TOL) attempts to solve the system of linear equations A*X=B
%   for X using the Jacobi method.

% Jacobi preconditioner
P=diag(diag(A)); %

% residual normalization
r0=norm(b);
if r0==0, r0=1; end

% first iteration
x=x0;
r=b-A*x; % The residual b - A*x
res(1)=norm(r); % The norm of the initial residual
iter=0;

while res(end)/r0 > tol && iter < nmax
    z=P\r; % Solve Pz=r
    x=x+z; % Update the solution
    r=b-A*x; % Recompute the residual
    iter=iter+1;
    res(iter+1)=norm(r); % Store the norm of the new residual
end

return

gauss_seidel.m:

function [x, iter, res]= gauss_seidel(A,b,x0,nmax,tol)
% GAUSS-SEIDEL iterative method
%   [X, Niter, Res] = GAUSS_SEIDEL(A,B,X0,NMAX,TOL) attempts to solve the system of linear equations A*X=B
%   for X using the Gauss-Seidel method.

% Gauss-Seidel preconditioner
P=tril(A); %

% residual normalization
r0=norm(b);
if r0==0, r0=1; end

% first iteration
x=x0;
r=b-A*x; % The residual b - A*x
res(1)=norm(r); % The norm of the initial residual
iter=0;

while res(end)/r0 > tol && iter < nmax
    z=P\r; % Solve Pz=r using forward substitution
    x=x+z; % Update the solution
    r=b-A*x; % Recompute the residual
    iter=iter+1;
    res(iter+1)=norm(r); % Store the norm of the new residual
end

return

b

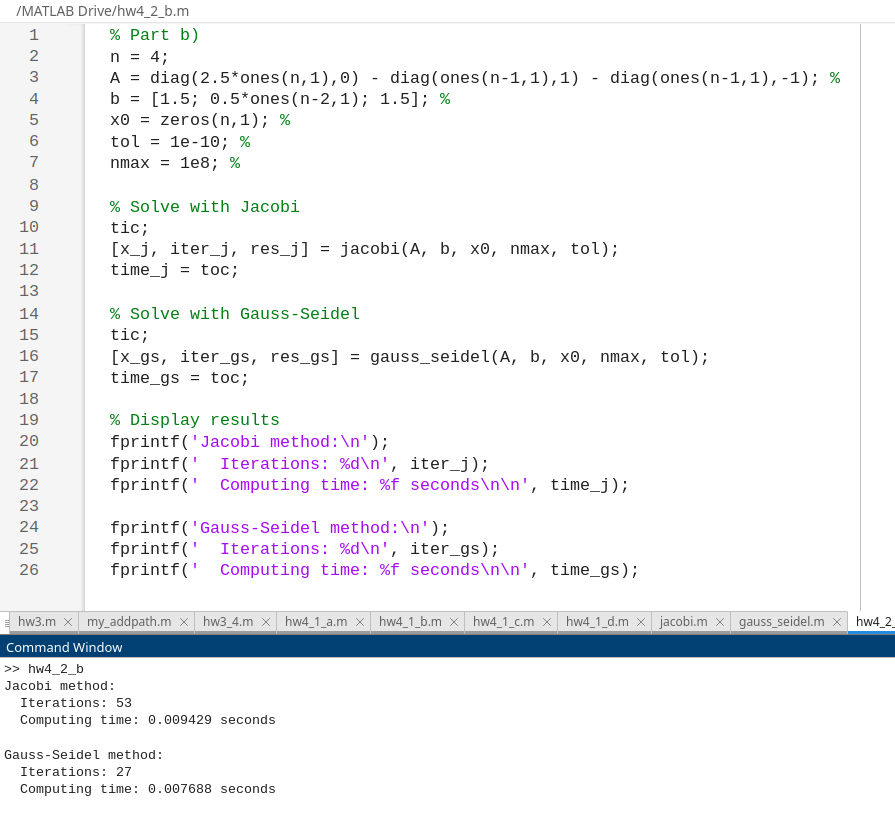
I solve the system for $n=4$ with the tridiagonal matrix $A$ having $2.5$ on the diagonal and $-1$ on the off-diagonals. The right-hand side is $b=(1.5,0.5,0.5,1.5)^{\top}$. The initial guess is $x^{(0)}=0$, tolerance is $10^{-10}$, and max iterations is $10^8$. I compare the number of iterations and computing time.

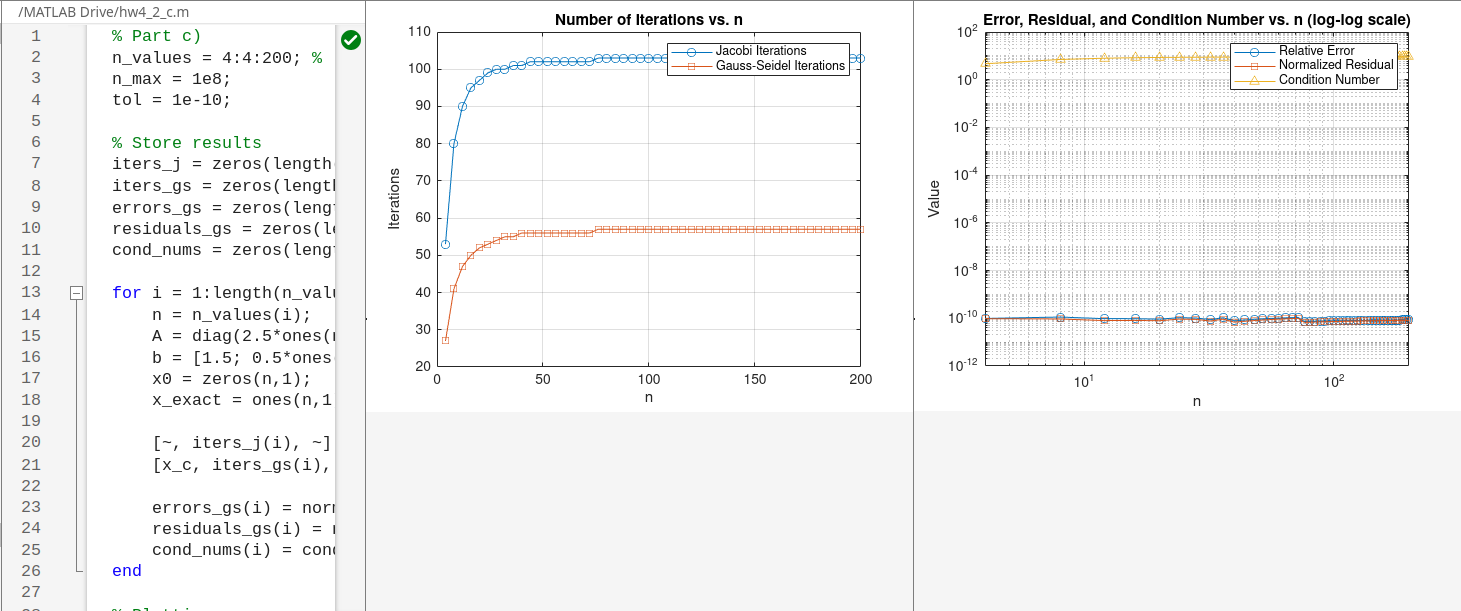
The matrix $A$ is strictly diagonally dominant since $|a_{ii}| = 2.5 > \sum_{j \neq i} |a_{ij}|$ for all rows. This property guarantees that both methods will converge. I expect Gauss-Seidel to converge faster.

### c The analysis is repeated for the same matrix family with $n$ varying from 4 to 200. The exact solution is $x=(1,...,1)^{\top}$. I plot the number of iterations, the relative error $||x-x_{c}||/||x||$, and the normalized residual $||b-Ax_{c}||/||b||$ versus $n$. I also examine how the condition number of A changes with n.

For this well-conditioned matrix (as shown in part e), the number of iterations grows very slowly with $n$. The condition number remains small and constant. The relative error and the normalized residual are very close in value, indicating that the residual is a good estimator of the error.

d

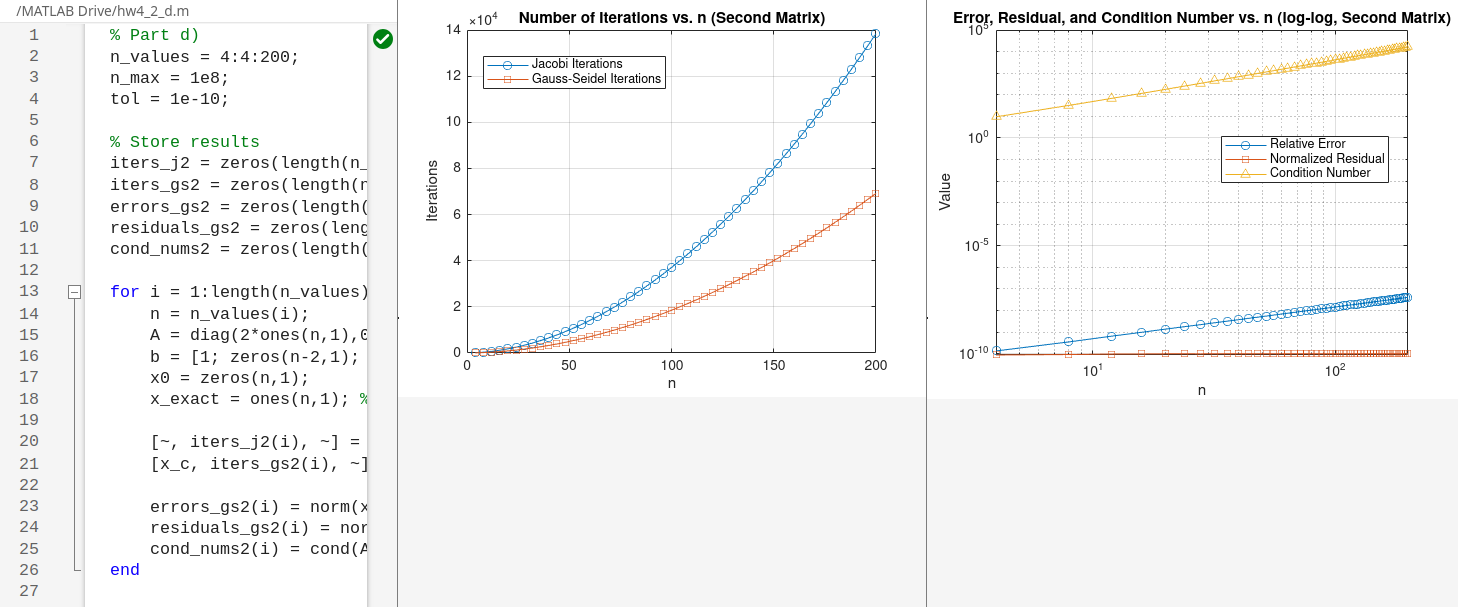
The analysis from (c) is repeated for the matrix $A$ with 2 on the diagonal and -1 on the off-diagonals , and $b=(1,0,…,0,1)^{\top}$. The exact solution is again $x=(1,…,1)^{\top}$. This matrix is only weakly diagonally dominant, so I expect slower convergence.

The number of iterations will grow much more rapidly with $n$. This is because, as shown in part (e), the condition number of this matrix grows quadratically with $n$, making the problem progressively harder to solve.

e

I use the given formula for the eigenvalues of a symmetric tridiagonal matrix $M$ with $a$ on the diagonal and $b$ on the off-diagonals:
$$ \lambda_{i}(M)=a+2b\cos\left(\frac{\pi i}{n+1}\right), \quad i=1,…,n $$
The condition number is $\kappa_2(A) = |\lambda_{max}|/|\lambda_{min}|$.

Case 1: Matrix from part (c)
Here, $a=2.5$ and $b=-1$. The eigenvalues are $\lambda_i = 2.5 - 2\cos(\frac{\pi i}{n+1})$.

• As $n\to\infty$, $\lambda_{max} \to 2.5 - 2(-1) = 4.5$.
• As $n\to\infty$, $\lambda_{min} \to 2.5 - 2(1) = 0.5$.

The condition number $\kappa(A)$ approaches a constant, $\kappa(A) \to 4.5 / 0.5 = 9$. This is consistent with the numerical results from part (c), explaining the fast and stable convergence.

Case 2: Matrix from part (d)
Here, $a=2$ and $b=-1$. The eigenvalues are $\lambda_i = 2 - 2\cos(\frac{\pi i}{n+1}) = 4\sin^2(\frac{\pi i}{2(n+1)})$.

• As $n\to\infty$, $\lambda_{max} \to 4\sin^2(\pi/2) = 4$.
• For large $n$, $\lambda_{min} = 4\sin^2(\frac{\pi}{2(n+1)}) \approx 4(\frac{\pi}{2(n+1)})^2 = \frac{\pi^2}{(n+1)^2}$.
  The condition number $\kappa(A) \approx \frac{4}{\pi^2/(n+1)^2} = O(n^2)$. This quadratic growth in the condition number is consistent with the numerical results from part (d), explaining the significant increase in iterations with $n$.