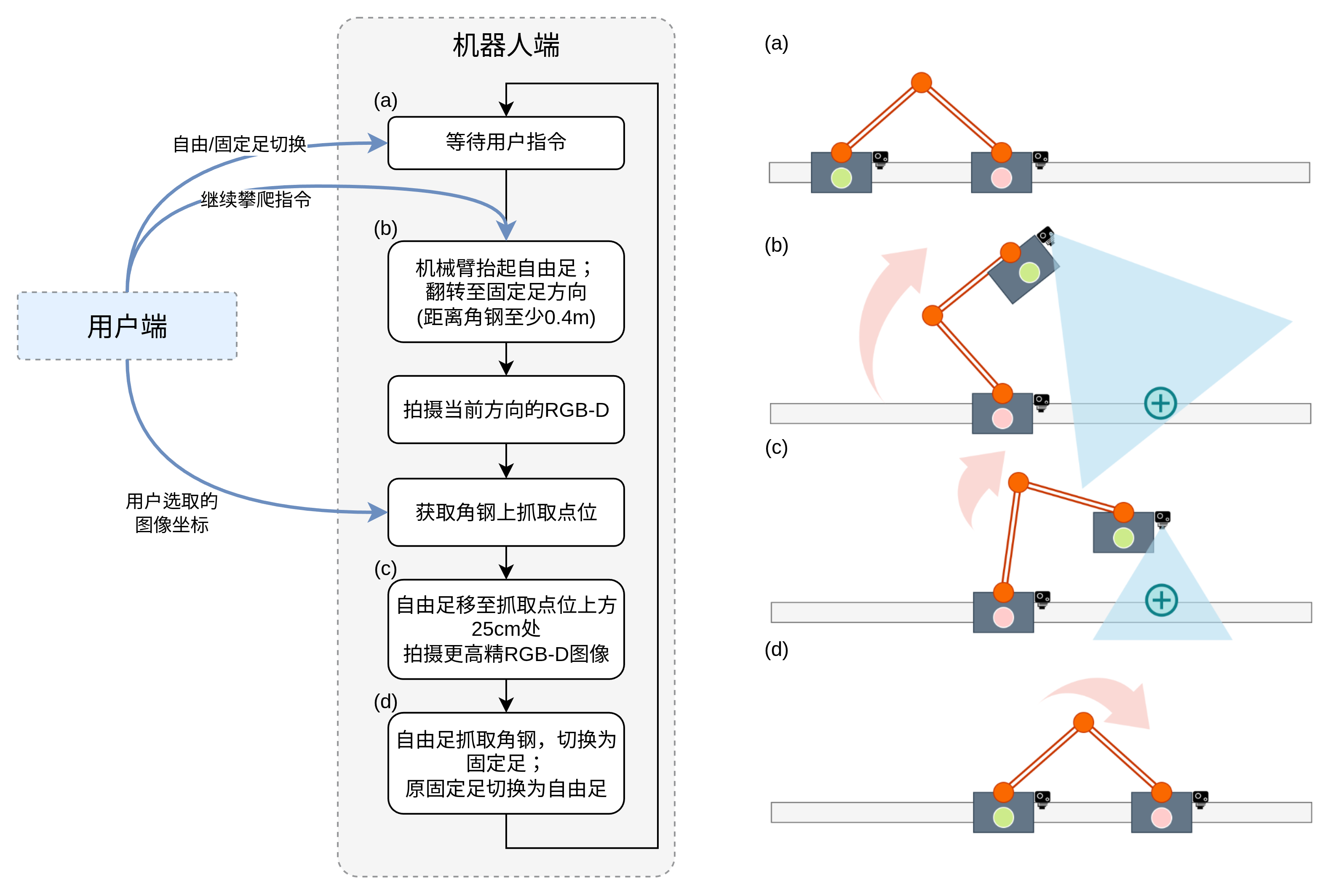
主要工作流
## 主要参数要求 在室外工作,输出至少720P深度与RGB图像 最好可以支持gmsl2接口 ### 电爪相机 拍摄"角钢选取"画面 - 距离要求:>0.4m - 精度误差要求:<10mm@1m 近距离拍摄"角钢抓取点"画面 - 距离要求:0.2-0.3m - 精度误差要求:<3mm@0.3m紧固相机
近距离拍摄”螺栓”
- 距离要求:<0.3m
- 精度误差要求:<1mm@0.3m
奥比中光
待选:
- Gemini 335Lg(作为电爪相机)
Intel
待选:
- D405(作为紧固相机)
近距离拍摄”螺栓”
待选:
- Gemini 335Lg(作为电爪相机)
待选:
- D405(作为紧固相机)
已知末端的位置和姿态,以及所有连杆的几何参数下,求解关节的位置。
特点:运算速度快(达到us级),通用性差,可以分为代数法与几何法进行求解。
串联机械臂有逆运动学解析解的充分条件是满足Pieper准则
即如果机器人满足两个充分条件中的一个,就会得到封闭解,这两个条件是:
特点:通用性高,但是求解速度较慢(ms级)。
除了一些特殊的机械臂构型外,机械臂逆运动学问题很难用解析解求解,因此在许多情况下会使用数值解求解。
Newton-Raphson(NR)是数值解的一种方法。它需要基本的雅可比矩阵(关节空间的速度映射到笛卡尔空间)。然而,当且仅当原始方程的函数具有逆函数,且原始方程可解时,NR方法才会成功。
雅可比矩阵求逆:
运动微分方程可得
求逆可得
**如果机械臂的初始关节状态$q(0)$已知,最终的目标关节位置可以通过速度对时间的积分进行计算。** 欧拉积分法 #### 多解 由于机械臂是多自由度、串联、多旋转轴的复杂系统,只要自由度不少于 6 或部分结构“折叠方式”不唯一,就会出现多个可行姿态。 • **6自由度机械臂**:通常最多 8 个逆解。 • **冗余机械臂(7自由度以上)**:无限多解,存在连续解族。 这类机械臂需要用优化方法选择最优解。主要是自我介绍,项目介绍,针对简历和scope的Q&A,较为顺利。
代码测是在小鹏自己的代码编写平台,带语言切换,输出,debug,类似力扣。题目是写一个计算路径数量的函数,考察递归算法。期待后续二面。
1 | # ===== 第一课时:函数的定义与使用 ===== |
Custom Robot URDF with Moveit2
使用solidworks URDF exporter.
需要注意不要使用
lock constrain限制零件位置。
https://moveit.picknik.ai/main/doc/examples/examples.html#integration-with-a-new-robot
首先克隆moveit2的示例仓库:
1 | git clone -b humble https://github.com/moveit/moveit2_tutorials |
编译项目colcon build,启动setup assistant:
1 | ros2 launch moveit_setup_assistant setup_assistant.launch.py |
随后按照教程配置SRDF。
配置完成后可以启动示例代码:
1 | ros2 launch panda_moveit_config demo.launch.py |
会将机械臂可视化并且拖动目标位置之后可以plan&execute。
涵盖范围:公交地铁,便利店
主打一个方便
涵盖范围:免税店,大型百货,便利店 (餐饮小店可能不支持)
支持ZFB退税
兑换一些以备不时之需
详细信息:
https://www.visitbusanpass.com/
预约:小红书Yacht G_Busan Pass
一、 自觉遵守团队活动纪律,尊敬师长、友爱同学,讲文明、懂礼貌,有诚信。
二、 按时、按量参加团队活动,不迟到,不早退,有病有事先请假(提前两周),不无故缺席(超过三次劝退)。
三、 认真刻苦、积极进取,正确对待学习中的困难和挫折,保持健康心理。
四、 爱护公共财物,规范使用各类活动器具,杜绝人身伤害事故及物品损坏事故的发生。
五、 学期内,活动缺席超过3次的(因身体突发疾病等特殊情况另行处理)的学员视作自动放弃课程活动
一、 自觉遵守团队活动纪律,尊敬师长、友爱同学,讲文明、懂礼貌,有诚信。
二、 按时、按量参加团队活动,不迟到,不早退,有病有事先请假(提前两周),不无故缺席(超过三次劝退)。
三、 认真刻苦、积极进取,正确对待学习中的困难和挫折,保持健康心理。
四、 爱护公共财物,规范使用各类活动器具,杜绝人身伤害事故及物品损坏事故的发生。
五、 学期内,活动缺席超过3次的(因身体突发疾病等特殊情况另行处理)的学员视作自动放弃课程活动。
https://mindplus.dfrobot.com.cn/catalog