始
点开了好多好多软件的年度报告。惊讶于原来今年是从那个时间点开始的,原来今年发生了这么多的事情。
代码
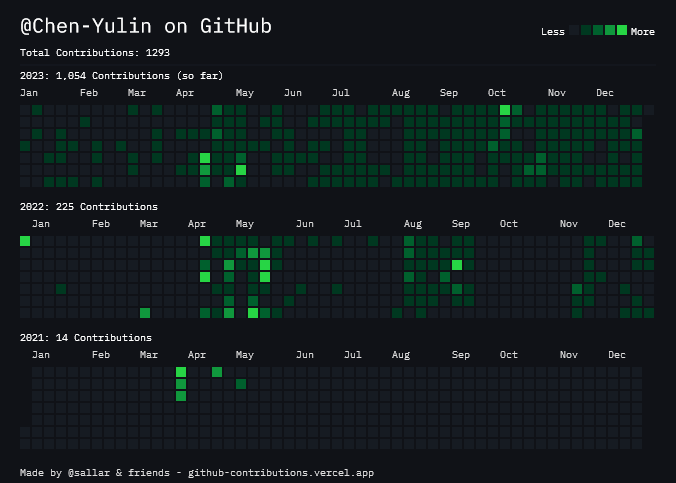
2023:1054 contributions on github
给现代空战模组进行了阶段性的收尾,工坊订阅人数到达了17k,有很多老外和群外的玩家都非常感兴趣,工坊首页中包含这个mod的载具也越来越多了,很高兴给这么多玩家的飞行载具注入了灵魂。
因为我原本是做木船出身,自然而然得就想着做一个适配二战海战的模组,事实上过程也非常顺利,将整个系统做得非常简明,用过都说好!但由于木船本身就是一个很小的圈子,所以订阅人数不多,刚到1k6。之后又爆肝加上了航母,舰载机系统,至此包含了二战海战中绝大部分的元素。
连续开发完两个mod也意识到玩家往往都会有个性需求,沙盒玩家更是如此,再加上我认为这两个mod有些地方存在共性,所以准备再开一个新坑,往游戏中加入数电的特色,玩家可以通过自己搭配原件来实现自己想要的效果,这样一来,海陆空现代战争的需求就都可以被满足。目前该mod仍然处于起步阶段。
科研
科研,也就那样啦,没发表什么paper,苦力活倒是干了不少。在电院的智能车实验室打杂,从零开发驾驶仿真平台,毕老师手下给ipp复现论文改代码,管理两个机器人小组的项目进度…希望明年能有意思一点(求师兄们捞捞啊)?不过虽说是打杂,倒也是积累了不少经验,譬如很多github的PR,ISSUE的开发习惯都是在电院的组里习得的,再就是也知道了骨骼模型的RNN是怎么一回事,啥是transformer。比起大一大二自己埋头做项目能习得的专项性知识更深入。大概也算是知道了当码仔大概是个什么样的生活(虽然从之前大二实习经历已经可见一斑)。写代码满足别人的需求有时候真的很无语,肯定给自己的idea写代码更有意思。
保研
保研确实是件头痛的事情,说实话我本来对此也没什么紧迫感,毕竟此前的政策一直是过GPA过3.0,保本院在名额上就不会有问题。然后就把被告知今年保研名额对于排名有要求,索性距离不大,努力一下。卷了一个学期成功加了0.15个绩点,保险起见还让毕老师写了一个reference(虽然感觉金力的推荐信也有点像reference)。历经两次meeting,两次小笔试,毕老师给了我一个研究生名额,他可能比较看重我之前做机器人的经验和自学这块的能力,可能还有这股愣头青的冲劲。参加完夏令营之后,就成了毕老师的硕士,他说是会按照博士的标准培养我,但其实我对于他手下硕博培养之间的区别也不慎了解。不过终归是求仁得仁。
恋爱
之前感觉我就是恋爱绝缘体,我知道,智者不入爱河。但就是突然看到永夜的天穹被阳光肆意地撕开了一角,而我也对那缕亮色,着迷了。在遇到gxy前我认为我不是一个会一见钟情的人,但显然我错得离谱。和她的第一次见面,我不敢看她,也不敢和她过多交流,但和她第二次见面的那个下午,基本就奠定,我已经在这场游戏中成为了猎物。我们发展地很快,我无可救药地爱上了这位向我敞开心扉的女孩,并确定了关系,我爱她的不屈,爱她有我没有的东西,爱她对我的包容,也爱上了这种被她喜欢,被她关心,被她倾听的感觉,这是我一直缺少的,但却又一直没意识到的东西。我意识到我已经回不去之前那种虚幻的,自给自足,“我就是我世界里的王”的心境了。恋爱如泡沫般易碎,美梦也会有梦醒的那一天,到时候我又应该如何自处。解决方案很简单,那就是一直一直和她在一起,但谈恋爱本身又是两个人之间的事情,不是我一个人能决定的。gxy真的是一个很好的女孩,但我真的很担心她某一天突然发觉我不是她在感情上需要的那个人,在太多太多事情上我没法给她足够的支持,在太多太多事情上我笨拙到令人发指。这就是一个我这个小男孩在初恋第73天心里会有的迷茫。


