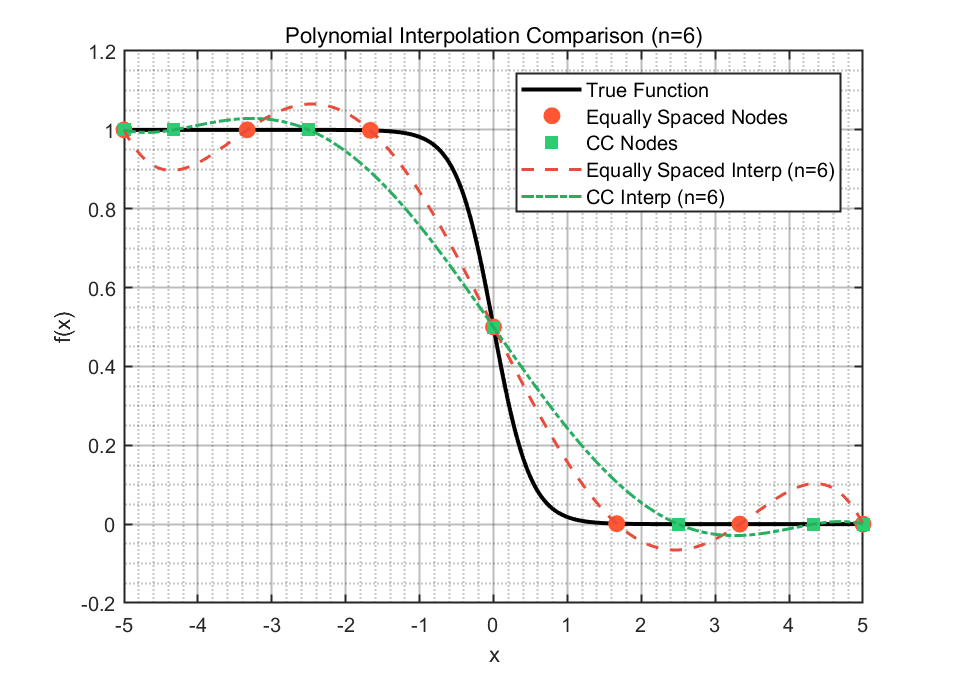
To approximate the function $$f(x) = \frac{1}{1 + \exp(4x)} $$on the interval [-5, 5], polynomial interpolation was performed using polynomials of degree n=6 and n=14. Two types of nodes were considered: equally spaced nodes and Clenshaw-Curtis nodes, the latter computed using the formula

